Modelling Series
Infinite response systems
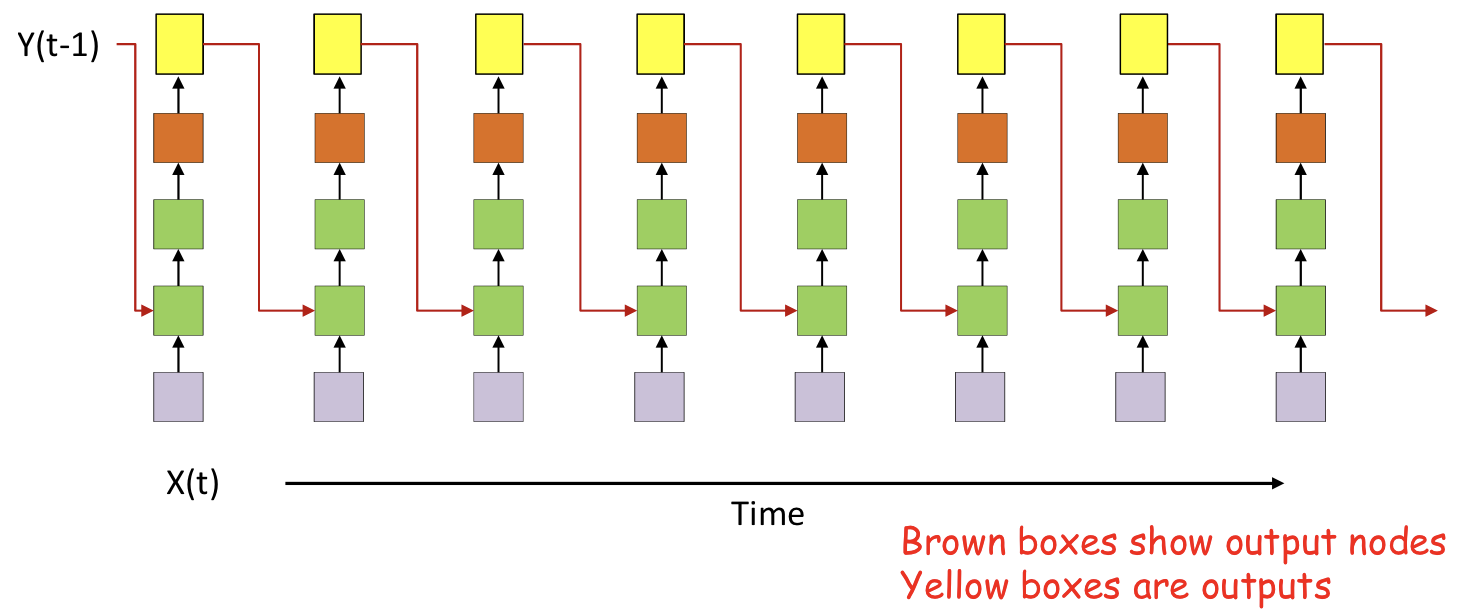
State-space model
ht=f(xt,ht−1)yt=g(ht)
- ht is the state of the network
- Model directly embeds the memory in the state
- State summarizes information about the entire past
- Recurrent neural network1
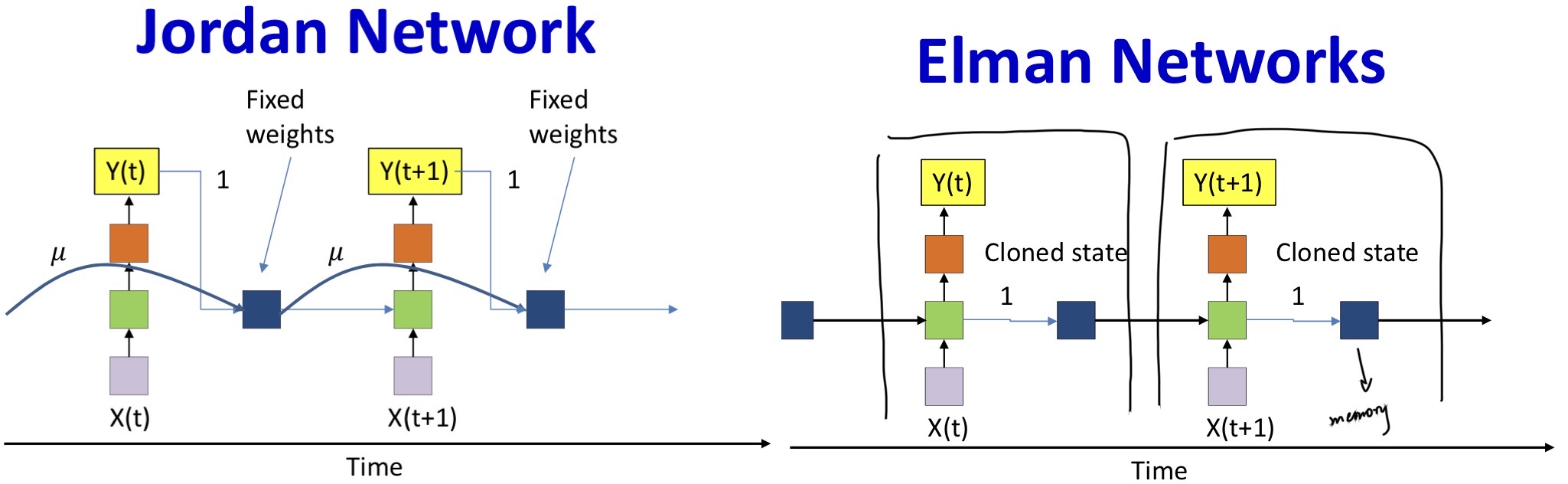
Variants
- All columns are identical
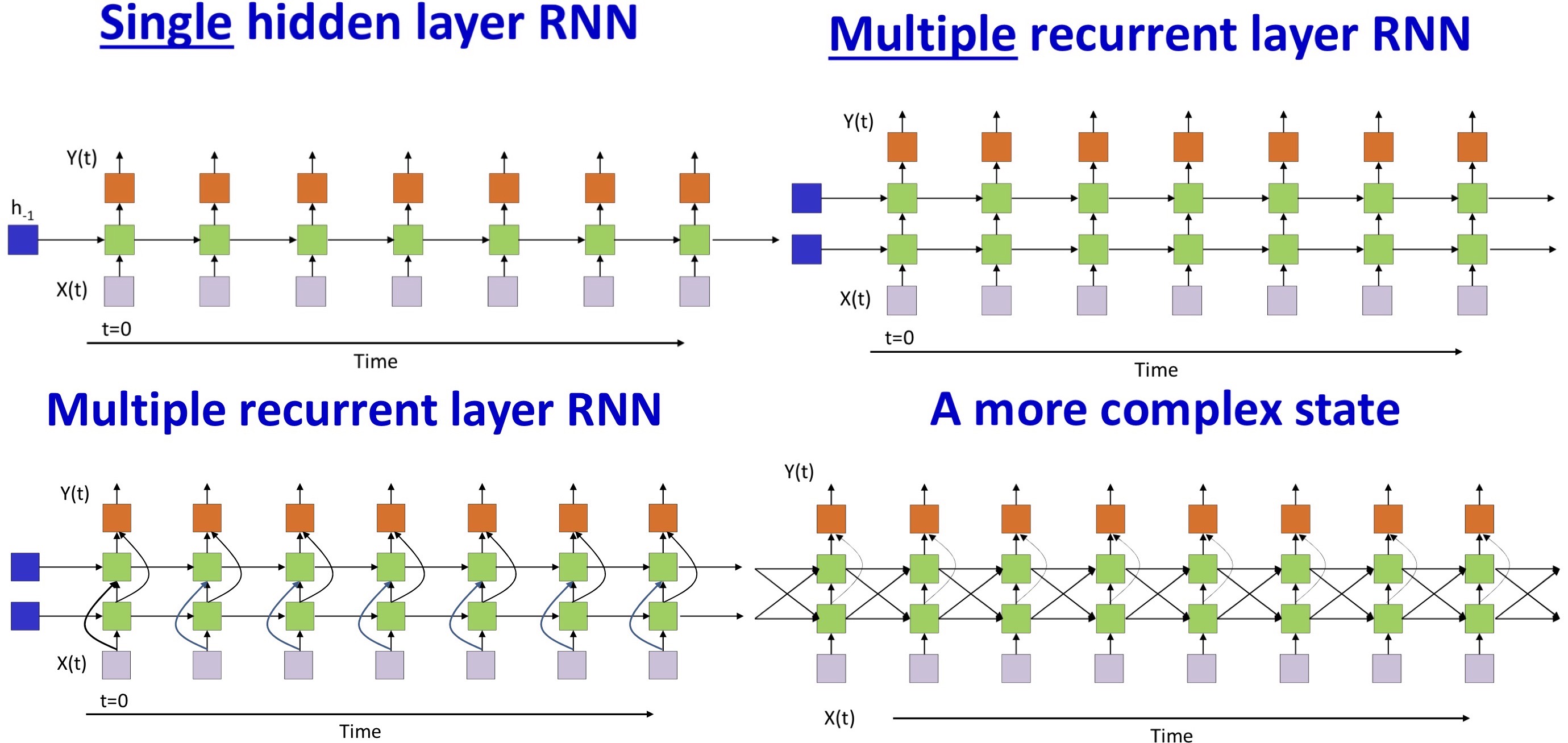
- The simplest structures are most popular
Recurrent neural network

Forward pass

Backward pass
- BPTT
- Back Propagation Through Time
- Defining a divergence between the actual and desired output sequences
- Backpropagating gradients over the entire chain of recursion
- Backpropagation through time
- Pooling gradients with respect to individual parameters over time
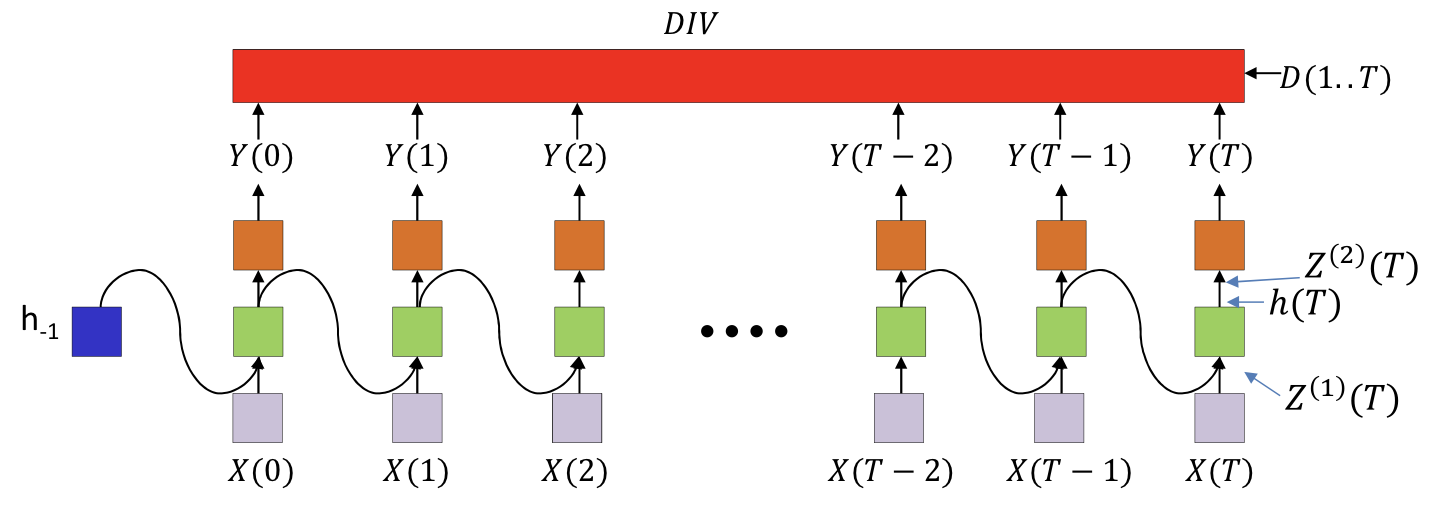
Notion
- The divergence computed is between the sequence of outputs by the network and the desired sequence of outputs
- DIV is a scalar function of a ..series.. of vectors
- This is not just the sum of the divergences at individual times
- Y(t) is the output at time t
- Yi(t) is the ith output
- Z(2)(t) is the pre-activation value of the neurons at the output layer at time t
- h(t) is the output of the hidden layer at time t
BPTT
- Y(t) is a column vector
- DIV is a scalar
- dY(t)dDiv is a row vector
Derivative at time T
Compute dYi(T)dDIV for all i
In general we will be required to compute dYi(t)dDIV for all i and t as we will see
- This can be a source of significant difficulty in many scenarios
Special case, when the overall divergence is a simple sum of local divergences at each time
- dYi(t)dDIV=dYi(t)dDiv(t)
Compute ∇Z(2)(T)DIV
∇Z(2)(T)DIV=∇Y(T)DIV∇Z(2)(T)Y(T)
For scalar output activation
- dZi(2)(T)dDIV=dYi(T)dDIVdZi(2)(T)dYi(T)
For vector output activation
- dZi(2)(T)dDIV=i∑dYj(T)dDIVdZi(2)(T)dYj(T)
Compute ∇h(T)DIV
W(2)h(T)=Z(2)(T)
dhi(T)dDIV=j∑dZj(2)(T)dDIVdhi(T)dZj(2)(T)=j∑wij(2)dZj(2)(T)dDIV
∇h(T)DIV=∇Z(2)(T)DIVW(2)
Compute ∇W(2)DIV
dwij(2)dDIV=dZj(2)(T)dDIVhi(T)
∇W(2)DIV=h(T)∇Z(2)(T)DIV
Compute ∇Z(1)(T)DIV
dZi(1)(T)dDIV=dhi(T)dDIVdZi(1)(T)dhi(T)
∇Z(1)(T)DIV=∇h(T)DIV∇Z(1)(T)h(T)
Compute ∇W(1)DIV
W(1)X(T)+W(11)h(T−1)=Z(1)(T)
dwij(1)dDIV=dZj(1)(T)dDIVXi(T)
∇W(1)DIV=X(T)∇Z(1)(T)DIV
Compute ∇W(11)DIV
dwii(11)dDIV=dZi(1)(T)dDIVhi(T−1)
∇W(11)DIV=h(T−1)∇Z(1)(T)DIV
Derivative at time T−1
Compute ∇Z(2)(T−1)DIV
∇Z(2)(T−1)DIV=∇Y(T−1)DIV∇Z(2)(T−1)Y(T−1)
For scalar output activation
- dZi(2)(T−1)dDIV=dYi(T−1)dDIVdZi(2)(T−1)dYi(T−1)
For vector output activation
- dZi(2)(T−1)dDIV=j∑dYj(T−1)dDIVdZi(2)(T−1)dYj(T−1)
Compute ∇h(T−1)DIV
dhi(T−1)dDIV=j∑wij(2)dZj(2)(T−1)dDIV+j∑wij(11)dZj(1)(T)dDIV
∇h(T−1)DIV=∇Z(2)(T−1)DIVW(2)+∇Z(1)(T)DIVW(11)
Compute ∇W(2)DIV
dwij(2)dDIV+=dZj(2)(T−1)dDIVhi(T−1)
∇W(2)DIV+=h(T−1)∇Z(2)(T−1)DIV
Compute ∇Z(1)(T−1)DIV
dZi(1)(T−1)dDIV=dhi(T−1)dDIVdZi(1)(T−1)dhi(T−1)
∇Z(1)(T−1)DIV=∇h(T−1)DIV∇Z(1)(T−1)h(T−1)
Compute ∇W(1)DIV
dwij(1)dDIV+=dZj(1)(T−1)dDIVXi(T−1)
∇W(1)DIV+=X(T−1)∇Z(1)(T−1)DIV
Compute ∇W(11)DIV
Back Propagation Through Time
dhi(−1)dDIV=i∑wij(11)dZj(1)(0)dDIV
dhi(k)(t)dDIV=j∑wi,j(k+1)dZj(k+1)(t)dDIV+j∑wi,j(k,k)dZj(k)(t+1)dDIV
dZi(k)(t)dDIV=dhi(k)(t)dDIVfk′(Zi(k)(t))
dwij(1)dDIV=t∑dZj(1)(t)dDIVXi(t)
dwij(11)dDIV=t∑dZj(1)(t)dDIVhi(t−1)
Algorithm

Bidirectional RNN
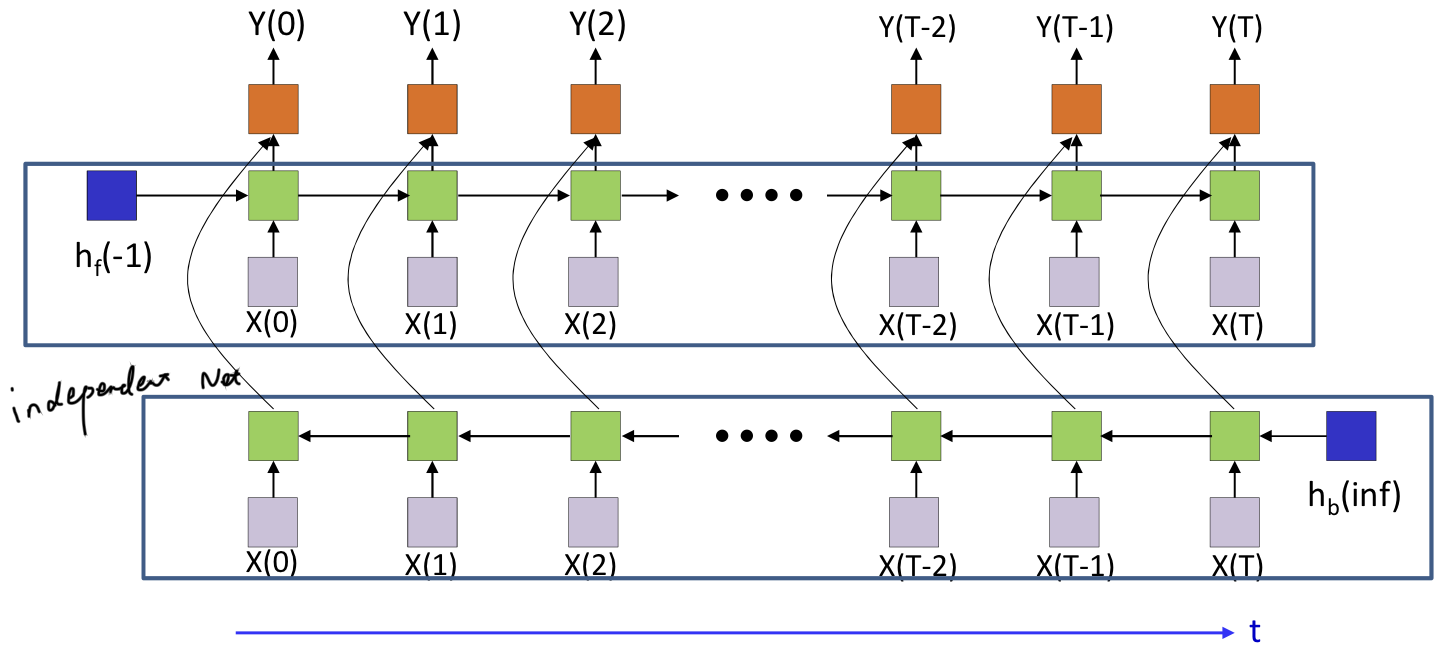
- Two independent RNN
- Clearly, this is not an online process and requires the entire input data
- It is easy to learning two RNN independently
- Forward pass: Compute both forward and backward networks and final output
- Backpropagation
- A basic backprop routine that we will call
- Two calls to the routine within a higher-level wrapper
1:The Unreasonable Effectiveness of Recurrent Neural Networks